Tout ce qui a été posté par chaps
-
Votre Dernier Achat
A ce prix là ça doit être le 256Go. Je l'ai depuis 1 mois, c'est une bombe !
-
Votre Dernier Achat
Perso j'ai pris celui-là : Samsung 830 256Gio, et je confirme que c'est le pied !
-
Votre Dernier Achat
Par contre si tu comptes acheter des jeux en dématérialisé, 16Go c'est vite rempli ... Perso j'ai préféré prendre tout de suite une 32Go pour être tranquille plus longtemps
-
Votre Dernier Achat
Ma Logitech MX900 bluetooth achetée en 2004 montre de belles traces d'usure, mais elle est toujours vaillante ! La qualité a baissé chez Logitech ?
-
Votre Dernier Achat
Une offre de remboursement de 50€ de la part de Sony, 150€ de bons d'achat de la part de mon employeur... J'ai craqué !
-
Votre Dernier Achat
Il parait qu'il n'y en a pas, que c'est en pénurie partout. Pourtant à Montgallet cet après-midi... Oui oui, au premier plan c'est bien une GTX690 !
-
Geforce GTX6XX
Depuis l’album : chaps
Des Geforce GTX670, GTX680 et GTX690 en vente ! -
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsDésolé RoCKets, étant au boulot j'ai fait ça rapidos sans prendre le temps de faire une recherche. Mea culpa
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsC'est sur MSX2
-
Le jeu du Screenshot
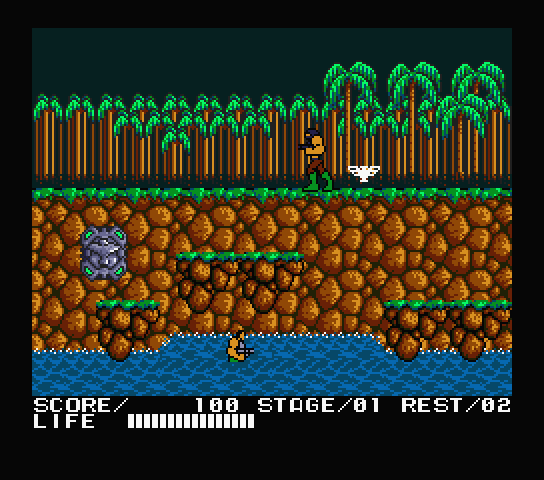
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsrefuznik Aussi connu sous le nom de Kontora, Probotector ou encore Gryzor ( beholder2)
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsSouvenirs, souvenirs !
-
ef5z4fe8zef6
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsCe ne serait pas Shadowcaster par hasard ?
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsNon non, c'est bien Bivouac. Sur Amiga apriori je dirais
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsC'est inexcusible plutôt, non ?
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsComme Flight Simulator quoi... Sauf que là, c'est toutes les touches plus toutes les combinaisons Shift+, Alt+, Crtl+, etc... qui sont utilisées !
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsMechwarrior 3 ? Si j'ai le point je le refilerai à Killator, je ne le mérite clairement pas
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsMechwarrior 2 ?
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsTest Drive ? Je ne sais pas si c'est le 1 ou le 2 par contre
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsLe forum PCI propose d'héberger les images, ce qui par la même occasion limite les problèmes d'image "IPB"... Dans votre profil, allez dans "Ma galerie", et roulez jeunesse !
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsYep, well done beholder2 ! Un jeu qu'il était bien, lui aussi
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsNop
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsJ'y ai passé du temps sur YDKJ, je connaissais par c½ur tous les "Jack Attack" ! Un nouveau screen :
-
a44zef44z6
-
Le jeu du Screenshot
chaps a répondu à un(e) sujet de superlapin62 dans Jeux vidéo, Consoles, Rétrogaming et Jeux occasionelsYou don't know Jack ! Haaa, les fameuses rimatologies... La vicieuse... Du grand art !